圖片:
開始也認(rèn)為二軸干不成,必須三軸,經(jīng)分析發(fā)現(xiàn)二軸可以完成。下面簡單分析下工件轉(zhuǎn)角和滑臺的位移關(guān)系。
先分析加工正方形。
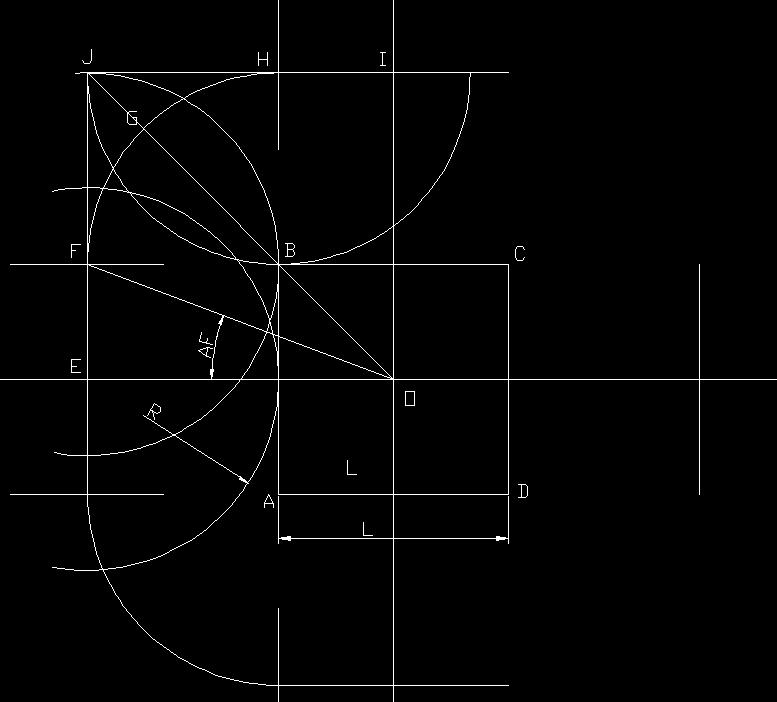
設(shè):正方形ABCD的邊長為L,沙輪的半徑為R,則沙輪中心到工件中心的基準(zhǔn) OE=R+L/2
加工是工件轉(zhuǎn)動,根據(jù)工件的轉(zhuǎn)角滑臺作對應(yīng)的移動。要求解的就是工件轉(zhuǎn)角和滑臺的位移關(guān)系。
根據(jù)運動的相對性,為方便分析,轉(zhuǎn)化成工件不動,沙輪繞工件轉(zhuǎn)動同時沿半徑方向移動。因為對稱,只要分析四分之一周期。
如圖,沙輪中心按 E-F-G-H-I.... 運動,即能切削出正方形。而在(F-G-H)圓弧段對應(yīng)加工點是B點尖角,基本不切削,可以讓沙輪離工件遠些,改成走E-F-j-H-I兩段直線,計算更方便。
實際只要計算一條邊,轉(zhuǎn)角從-90度 到 +90度 (計算要改用弧度計算)
如 轉(zhuǎn)角為 AF,基準(zhǔn)距離為 OE=R+L/2,相對于基準(zhǔn)距離的滑臺位移 S
-PI/4 <= AF <= PI/4 PI=3.141592 (弧度)
工件轉(zhuǎn)角對應(yīng)的工件與沙輪的中心距 OF
OF=OE/COS(AF)=(R+L/2)/COS(AF)
相對于基準(zhǔn)距離的滑臺位移 S
S=OF-OE=(R+L/2)/COS(AF)-(R+L/2)=(R+L/2)/(1/COS(AF)-1)
這就是需要的關(guān)系公式,我只能提供這些了,其他要你自己解決。
橢圓就更復(fù)雜,搞這項目要有數(shù)學(xué)基礎(chǔ)
當(dāng)然加工時工件轉(zhuǎn)速不能快,這是由磨削加工決定的,所以滑臺速度也不會快。